Dimensions in Light

_____________________________________________

______________________________________________
Isaac Newton
From 1670 to 1672 lectured on optics.

During this period he investigated the refraction of light, demonstrating that a prism could decompose white light into a spectrum of colours, and that a lens and a second prism could recompose the multicoloured spectrum into white light. He also showed that the coloured light does not change its properties, by separating out a coloured beam and shining it on various objects. Newton noted that regardless of whether it was reflected or scattered or transmitted, it stayed the same colour.

Thus the colours we observe are the result of how objects interact with the incident already-coloured light, not the result of objects generating the colour. For more details, see Newton's theory of colour. Many of his findings in this field were criticized by later theorists, the most well-known being Johann Wolfgang von Goethe, who postulated his own colour theories.

A replica of Newton's 6-inch reflecting telescope of 1672 for the Royal Society.
From this work he concluded that any refracting telescope would suffer from the dispersion of light into colours, and invented a reflecting telescope (today known as a Newtonian telescope) to bypass that problem. By grinding his own mirrors, using Newton's rings to judge the quality of the optics for his telescopes, he was able to produce a superior instrument to the refracting telescope, due primarily to the wider diameter of the mirror. (Only later, as glasses with a variety of refractive properties became available, did achromatic lenses for refractors become feasible.) In 1671 the Royal Society asked for a demonstration of his reflecting telescope. Their interest encouraged him to publish his notes On Colour, which he later expanded into his Opticks. When Robert Hooke criticised some of Newton's ideas, Newton was so offended that he withdrew from public debate. The two men remained enemies until Hooke's death.

In one experiment, to prove that colour perception is caused by pressure on the eye, Newton slid a darning needle around the side of his eye until he could poke at its rear side, dispassionately noting "white, darke & coloured circles" so long as he kept stirring with "ye bodkin."

Newton argued that light is composed of particles, but he had to associate them with waves to explain the diffraction of light. Later physicists instead favoured a purely wavelike explanation of light to account for diffraction.

Today's quantum mechanics restores the idea of "wave-particle duality", although photons bear very little resemblance to Newton's corpuscles (e.g., corpuscles refracted by accelerating toward the denser medium).


_____________________________________________________
(dubious assertion—see talk page)
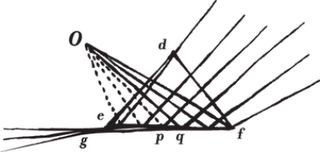
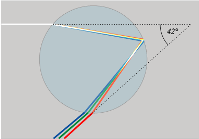
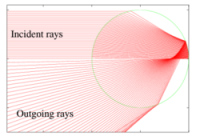
Newton is believed to have been the first to explain precisely the formation of the rainbow from water droplets dispersed in the atmosphere in a rain shower. Figure 15 of Part II of Book One of the Opticks shows a perfect illustration of how this occurs.


_____________________________________________________

Before Max Planck suggested that light is quantized, optics consisted mainly of the application of electromagnetism and its high frequency approximations to light.

Classical optics divides into two main branches:
geometric optics and physical optics.

Geometric optics, or ray optics, describes light propagation in terms of "rays". Rays are bent at the interface between two dissimilar media, and may be curved in a medium in which the refractive index is a function of position. The "ray" in geometric optics is an abstract object which is perpendicular to the wavefronts of the actual optical waves. Geometric optics provides rules for propagating these rays through an optical system, which indicates how the actual wavefront will propagate. Note that this is a significant simplification of optics, and fails to account for many important optical effects such as diffraction and polarization.

Geometric optics is often simplified even further by making the paraxial approximation, or "small angle approximation." The mathematical behavior then becomes linear, allowing optical components and systems to be described by simple matrices. This leads to the techniques of Gaussian optics and paraxial raytracing, which are used to find first-order properties of optical systems, such as approximate image and object positions and magnifications.

Gaussian beam propagation is an expansion of paraxial optics that provides a more accurate model of coherent radiation like laser beams. While still using the paraxial approximation, this technique partially accounts for diffraction, allowing accurate calculations of the rate at which a laser beam expands with distance, and the minimum size to which the beam can be focused.

Gaussian beam propagation thus bridges the gap between geometric and physical optics.

Physical optics models the propagation of complex wavefronts through optical systems, including both the amplitude and the phase of the wave. This technique, which is usually applied numerically on a computer, can account for diffraction, interference, and polarization effects, as well as aberrations and other complex effects. Approximations are still generally used, however, so this is not a full electromagnetic wave theory model of the propagation of light. Such a full model would (at present) be too computationally demanding to be useful for most problems, although some small-scale problems can be analyzed using complete wave models.
_____________________________________________________
Newton the Alchemist by Plato
The Chemistry of Isaac Newton Symbols Guide @ Indiana edu
______________________________________________________